음악은 박자 그리고 선율과 화음이 골고루 섞여 하나의 곡을 완성시킨다. 또한 모든 음악적 표현은 이름이 따라 붙는다. 이를 이해하고 있어야 여러 종류의 화음, 음정, 스케일 등을 설명할 수 있고 또 구별해낼 수 있다.
이전에는 음의 위치와 위치에 따른 음이름을 알아봤다면, 이번에는 동시에 울리는 서로다른 음 즉, 음정에 대해 알아볼 것이다.
15. 음정(Interval)
음정은 음악이론에서 두 음의 높이 차이를 말한다. 쉽게 말해 두 음 사이의 거리를 나타내는 용어이다. 두 음이 시간적 차이를 두고 순차적으로 울리는 것을 선율적 음정이라하고, 동시에 울리는 것을 화성적 음정이라고 한다.
1 ) 도수
음 사이의 간격에 대한 '도수' 는 음이름에 따라 결정된다. C, D, E, F, G, A, B, C / E, F, G, A, B, C, D, E 순번에 따라 도수를 계산한다.

예를들어 C를 기준으로하면(위의 그림과 동일한 설명이다.)
- C는 첫번째 순번이자 같은 음으로 도수는 1도이다.
- D는 두 번째 순번이므로 도수는 2도이다.
- E는 세 번째 순번이므로 도수는 3도이다.
- F는 네 번째 순번이므로 도수는 4도이다.
- G는 다섯 번째 순번이므로 도수는 5도이다.
- A는 여섯 번째 순번이므로 도수는 6도이다.
- B는 일곱 번째 순번이므로 도수는 7도이다.
- 한 옥타브 위 C는 여덟 번째 순번이므로 도수는 8도이다.

피아노의 흰 건반을 생각하면 쉽다. 두 개의 음을 동시에 쳤을 때 두 음을 흰 건반의 간격으로 따지면 된다.

피아노를 모르는 경우 손가락이나 머릿속으로 두 음의 도수를 따질 때 아래음을 기준으로 계이름을 순서대로 윗음에 도달할 때까지 세어나가면 된다.
지금까지 배운 도수 세는 방법은 그저 음과 음 사이의 거리만을 따지는 방법으로, 도수에 성질까지 더해야 비로소 '음정'을 정확하게 배우는 것이라고 할 수 있다.
다시말해 음정은 '도수'라는 단위로 음의 떨어져 있는 정도를 계산하고, 같은 도수 안에서도 실제 음과 음의 간격에 따라 도수 앞에 성질을 추가적으로 표기해준다.
=> '성질 + 도수'
예)
한글 : 완전 5도, 장3도, 증4도, 단2도 등..
영어 : Perfect 5th(P5), Major 3rd(M3), Augmented 4th(A4), minor 2nd(m2)
음정의 종류는 완전 음정(Perfect Interval), 장음정(Major Interval), 단음정(minor Interval), 증음정(Augmented Interval), 감음정(Diminished Interval)으로 5종류가 있다.
음정의 성질을 크게 두 개로 분류하면 온음계의 음정과 반음계의 음정으로 나눌 수 있다.
2 ) 온음계적 음정(Dianonic Interval)
음과 음 사이의 도수를 정하고 그 정해진 도수를 기반으로 두 음의 정확한 간격을 나타내기 위해 도수 앞에 성질을 표기한다.
장음계의 계이름을 기준으로 두 음 모두 변화표를 붙이지 않은 상태에서 만들어지는 모든 음정을 온음계의 음정이라고한다.
1, 4, 5, 8도 간격의 음정은 완전(Perfect) 성질을 붙여 음정을 완성한다. 완전1도, 완전4도와 같이 표기한다.
2, 3, 6, 7도 간격의 음정은 장(Major) 성질을 붙여 음정을 완성한다. 장3도, 장7도와 같이 표기한다.

완전음정과 장음정에 온음과 반음관계를 기준으로 단음정, 증음정, 감음정이 만들어진다.
변화표가 있지 않아도 두 음 사이에 반음이 완전음정과 장음정의 반음의 개수가 다르다면 단, 증, 감음정이 되는 것이다.
완전음정과 장음정에 반음의 개수에 따라 달라지는 성질은 다음과 같이 표로 정리하였다.

- 완전음정의 반음의 개수는 다음과 같다.
▶ 1도 : 0개(두 음정이 같은음이기 때문에 반음은 없다.)
▶ 4도 : 1개(예 : 도-파 안에 있는 반음은 미-파 1개이다.)
▶ 5도 : 1개(예 : 도-솔 안에 있는 반음은 미-파 1개이다.)
▶ 8도 : 2개(예 : 도-도 안에 있는 반음은 미-파, 시-도 2개이다.)

- 장음정의 반음의 개수는 다음과 같다.
▶ 2도 : 0개
▶ 3도 : 0개
▶ 6도 : 1개(예 : 도-라 6도 안에 있는 반음은 미,파 1개이다.)
▶ 7도 : 1개 (예 : 도-시 7도 안에 있는 반음은 미-파 1개이다.)

- 단음정 반음의 개수는 다음과 같다.
▶ 2도 : 1개(예 : 미-파 안에 있는 반음은 미-파 1개이다.)
▶ 3도 : 1개(예 : 라-도 안에 있는 반음은 시-도 1개이다.)
▶ 6도 : 2개(예 : 미-도 안에 있는 반음은 미-파, 시-도 2개이다.)
▶ 7도 : 2개(예 : 시-라 안에 있는 반음은 시-도, 미-파 2개이다.)
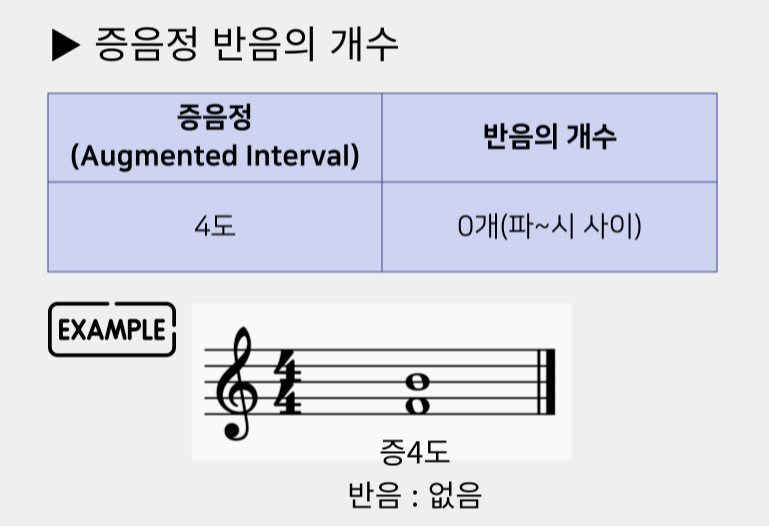
- 증음정 반음의 개수는 다음과 같다.
▶ 4도 : 0개(변화표가 없는 온음계의 음정에서의 증4도는 파-시 하나뿐이다. 파-시 사이에는 반음이 없다.)
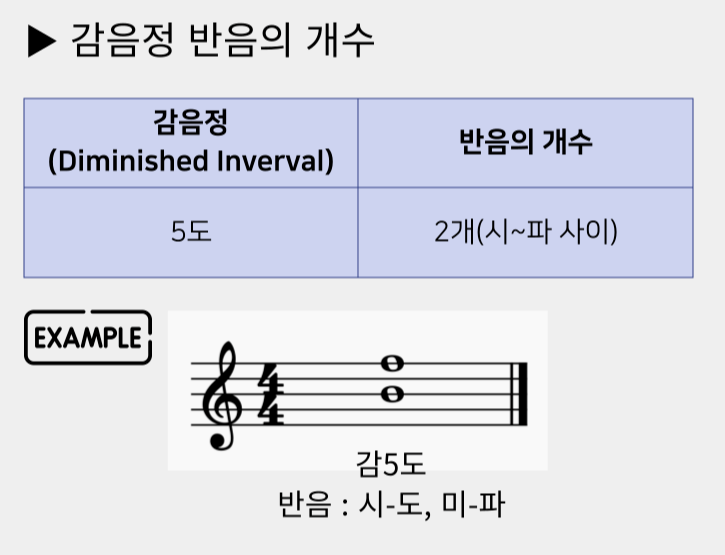
- 감음정 반음의 개수는 다음과 같다.
▶ 5도 : 2개(변화표가 없는 온음계의 음정에서의 감5도는 시-파 하나뿐이다. 시-파 사이에는 시-도, 미-파 2개의 반음이 있다.)
3 ) 반음계의 음정
반음계의 음정은 변화표가 포함된 모든 음의 간격을 말한다.
즉, 기준음이나 비교음에 샵(♯)이나 플랫(♭)이 붙게 되어 음 사이의 간격이 더 넓어지거나 좁아지게 되면 도수는 변하지 않지만 장(Major) 성질은 단(minor), 감(diminished), 증(augmented) 성질로 변하고, 완전(Perfect) 성질은 감(diminished), 증(augmented)과 같은 성질로 변하게 된다.
음계 위의 존재하는 모든 음의 간격의 성질 변화를 그림으로 표기하여 한 눈에 보기 쉽게 정리하면 다음과 같다.
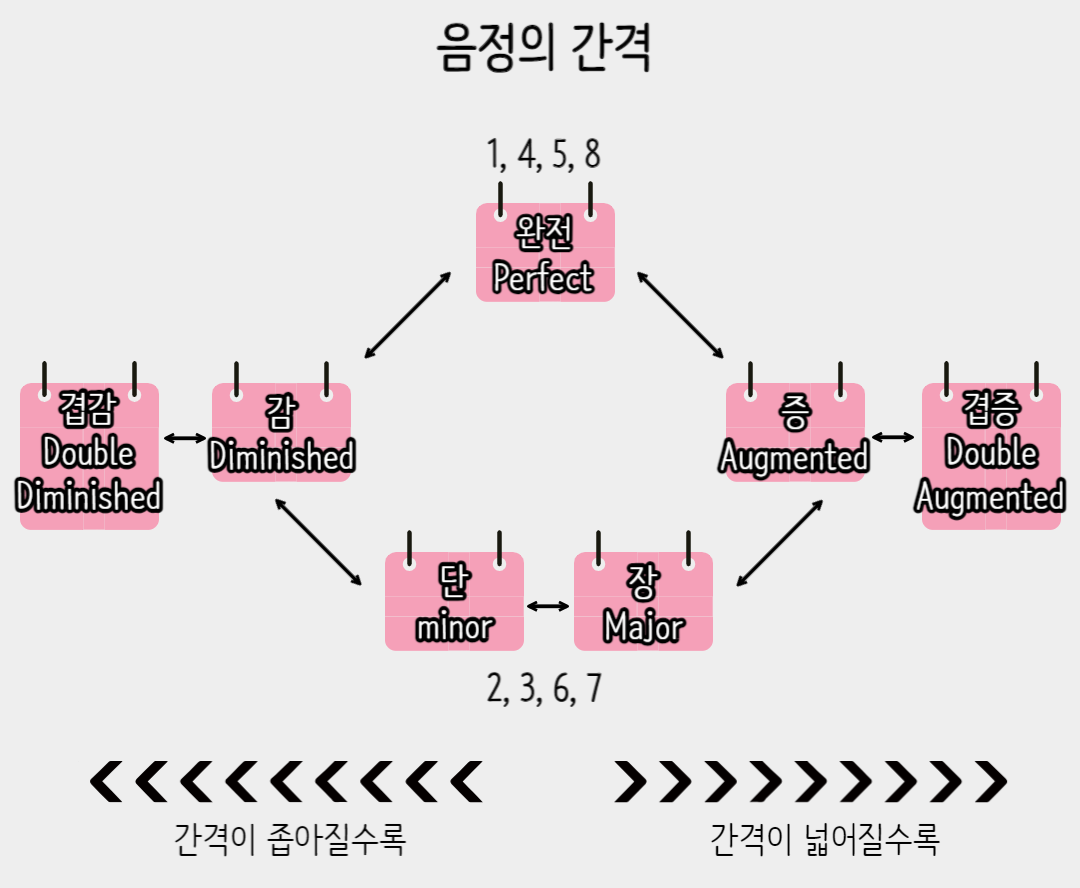
음정변화의 예를 보면 아래와 같다.
예 1)

> 도♭ - 파 : 도-파는 완전4도이지만 '도'에 있는 내림표로 인해 간격이 늘어났기 때문에 증4도가 된다.
예 2)

> 솔 - 시♭ : 솔-시는 장3도이지만 '시'에 있는 내림표로 인해 간격이 좁아져 단3도가 된다.
예 3)
조표가 있는 음정의 변화를 계산하는 경우는 음정을 먼저 계산한 후 조표를 적용하여 계산한다.
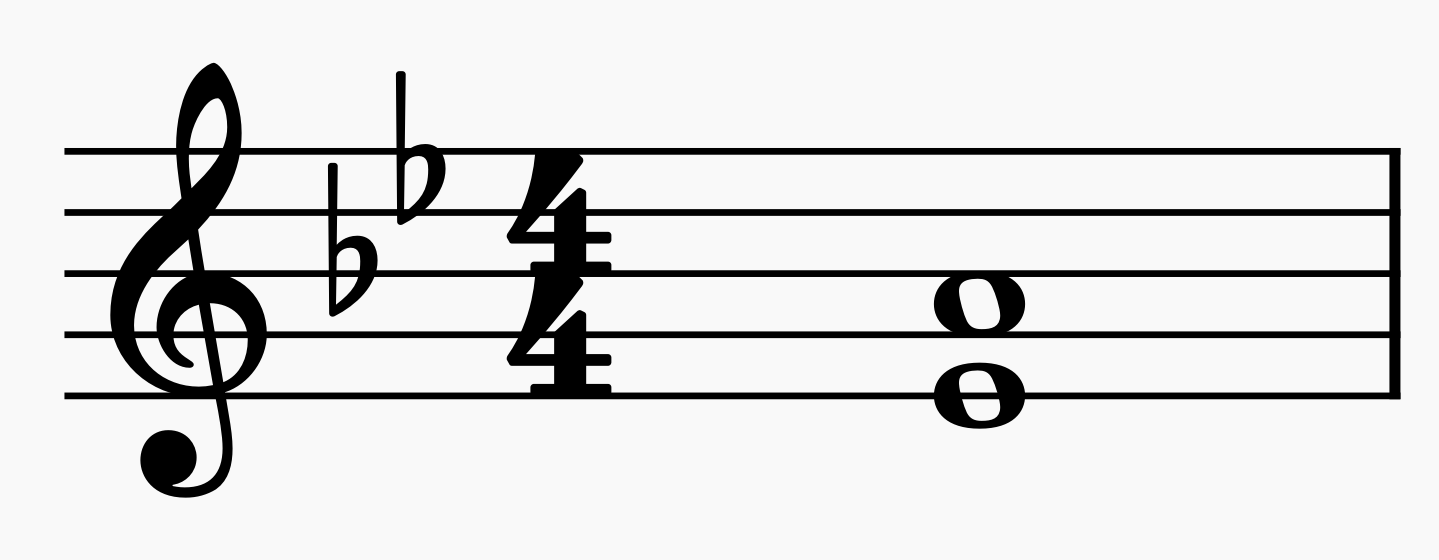
> ① 음정의 수는 4이고 4도는 완전음정이다. = 완전4도
② '미-파' 관계로 반음이 하나 존재한다. 완전4도는 반음이 한 개 존재한다. = 완전4도
③ 조표로 인해 '미'에 내림표가 붙어 간격이 반음 넓어졌다. = 증4도
※ 결과 : 증4도
4 ) 자리바꿈음정(Inversion)
자리바꿈음정이란 말 그대로 음정의 위 아래의 자리를 바꾸는 것을 말한다. 다른 말로는 전위음정이라고도 한다.
자리바꿈음정은 쉽게 계산하는 공식이 있다.
① 9 - 원음정 = 자리바꿈음정
② 성질의 변화
> 완전 - 완전
> 장 - 단
> 증 - 감
> 겹증 - 겹감
예 1)

- '미-도'는 반음이 2개이므로 단6도로 구성된다.
- 자리바꿈음정 계산하는 방법대로 계산하게 될 경우
① 9 - 6 = 3으로 3도이고
② 단음정은 장음정으로 바뀌므로
※ '미-도'인 단6도의 자리바꿈음정은 '도-미'인 장3도가 된다.
예 2)
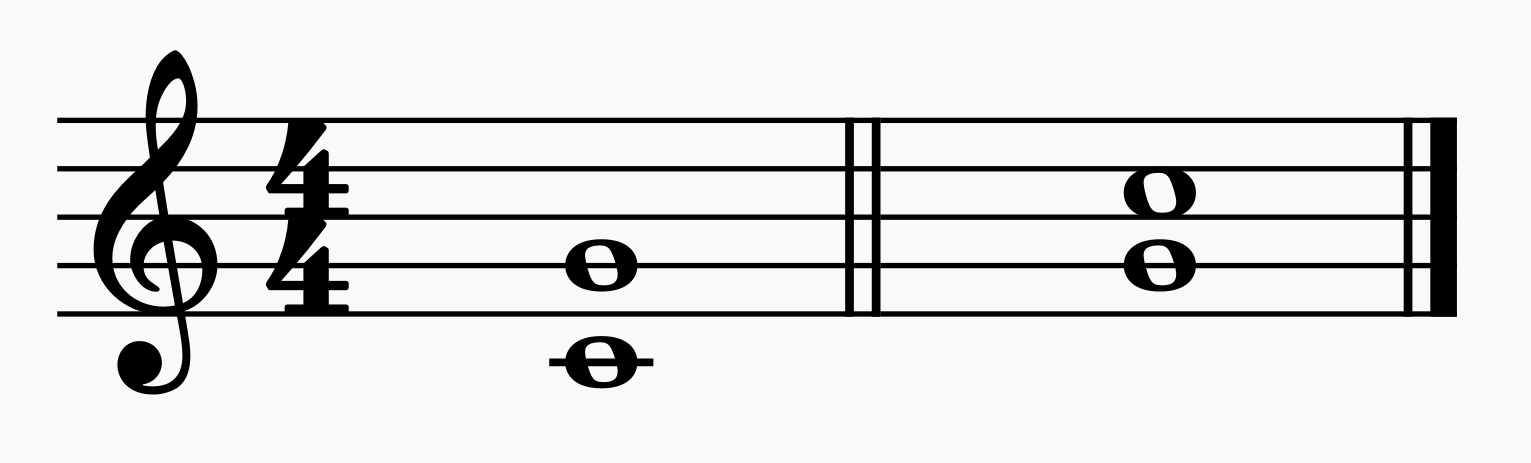
- '도-솔'은 반음이 1개인 5도로 완전5도로 구성된다.
- 자리바꿈음정을 계산하면
① 9 - 5 = 4으로 4도이고
② 완전음정은 그대로 완전음정 이므로
※ '도-솔'인 완전5도의 자리바꿈음정은 '솔-도'인 완전4도가 된다.
5 ) 겹음정(Compound Interval)
겹음정은 1옥타브가 넘는 9도 이상의 음정을 말한다. 겹음정은 음과 음 사이의 간격이 1옥타브가 넘을 뿐 원래의 음정의 성질과 동일하다.
겹음정은 음정의 아래 또는 위의 음을 같은 옥타브로 이동하여 음정을 구한다. 그 후 구한 음정에 7을 더해서 음정을 표기하거나 '1oct와 N도'라고 한다.(이 때 N도는 장3도, 완전5도 등을 말한다.)
예 )

- 주어진 '도-1oct 미'는 '미'를 1옥타브 내려 계산하면 아래 그림과 같다.

- '도-미'로 3도이고 반음은 포함되어있지 않기 때문에 장3도가 된다.
※ 장3도에 +7을 하면 '장10도'가 된다. 혹은 '1oct와 장3도'라고 한다.
6 ) 음정의 어울림(어울림음정과 안어울림음정)
음정은 자연배음의 원리를 따라 어울림음정(협화음정)과 안어울림음정(불협화음정)으로 나눌 수 있다.
우리가 일상속에서 잘 쓰는 단어 중에 하나가 '불협화음'이다. 어떤 음악 연주를 들을 때 귀 속에 들리는 음들이 자연스럽지 못하고 거슬리게 만드는 음이 있다던지, 듣기 엉망인 연주를 들을 때 우리는 '이 노래는 불협화음이다.'라고 하기도 한다.
이미 우리는 협화음과 불협화음을 알고 있는 것이다.
어울림음정(협화음정)은 우리가 듣기에도 편안함과 안정감을 느끼는데에 반해 안어울림음정(불협화음정은) 긴장감과 불안한 느낌을 주는 음이다.
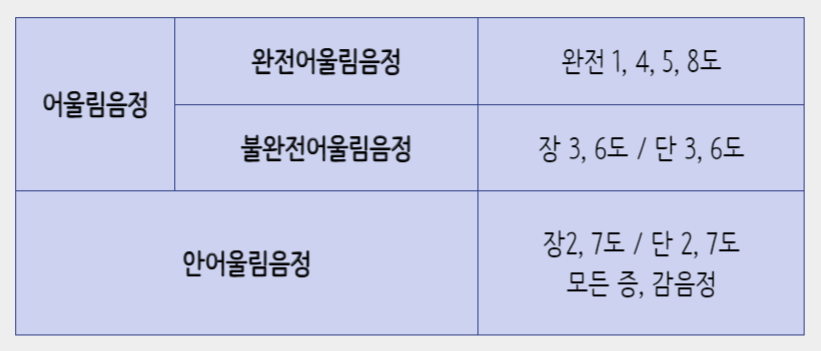
또한 어울림음정(협화음정)에서도 완전어울림음정과 불완전어울림음정으로 세분화해서 나눌 수 있다.
♥ 음정 파트는 가장 기초이면서도 어려운 파트이기 때문에 여러번 나누어 보면서 익히는게 중요하다. 어렵지만 잘 익혀두면 유용하게 사용되니 포기하지말고 배우기를 바란다.
'음악 > 화성학' 카테고리의 다른 글
| [악보 보는 방법 5] 셈여림 기호, 늘임표, 반복기호 (0) | 2023.11.02 |
|---|---|
| [악보 보는 방법 4] 박자표, 마디, 붙임줄과 이음줄, 기보법, 메트로놈 (0) | 2023.10.31 |
| [악보 보는 방법 3] 옥타브, 음표와 쉼표, 점음표, 셋잇단음표 (0) | 2023.10.26 |
| [악보 보는 방법 2] 음이름과 계이름, 사이음, 온음과 반음, 딴이름 한소리, 조표와 임시표 (1) | 2023.10.25 |
| [악보 보는 방법 1] 악보와 보표, 보표의 종류, 높은음자리표, 낮은음자리표 (2) | 2023.10.20 |



